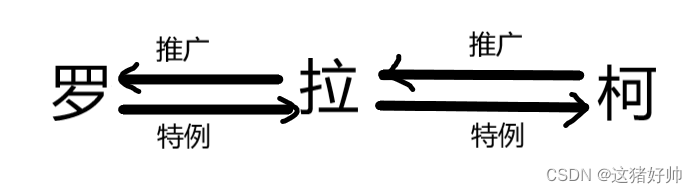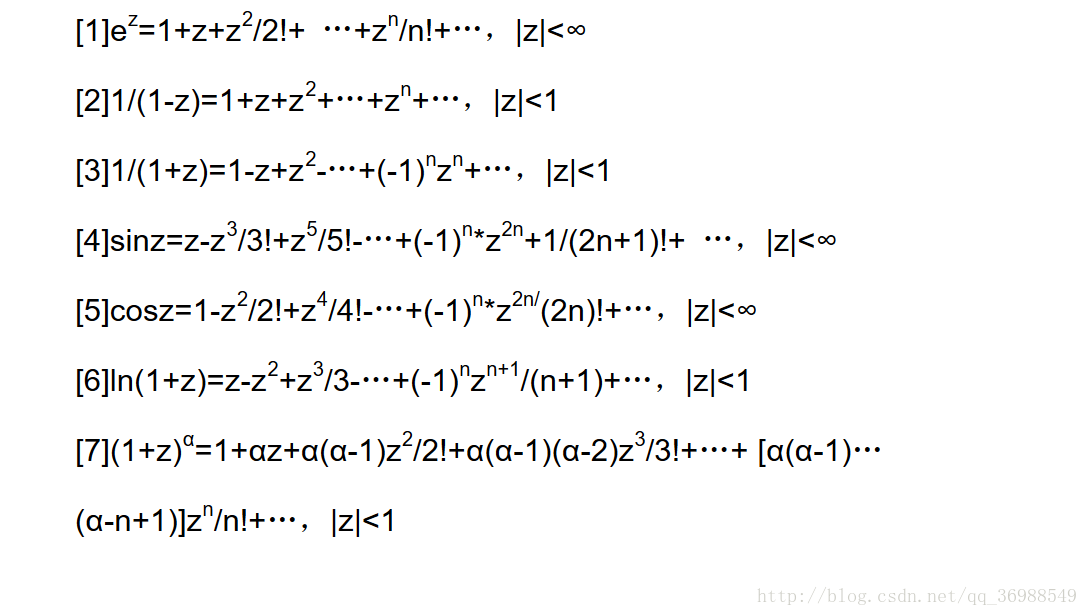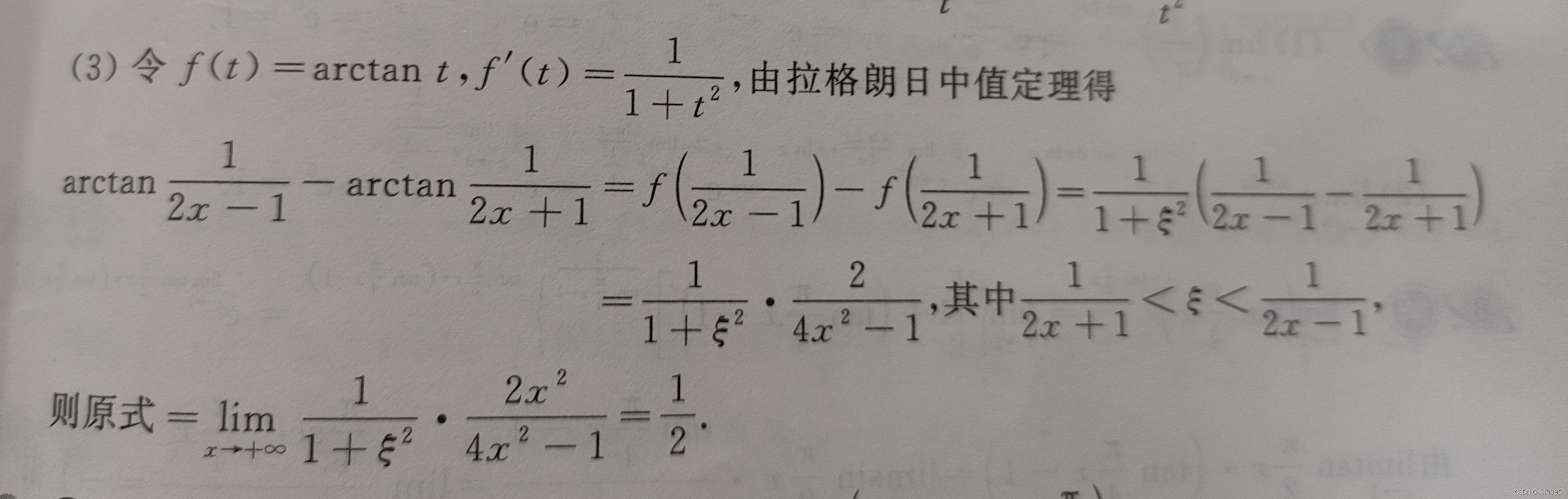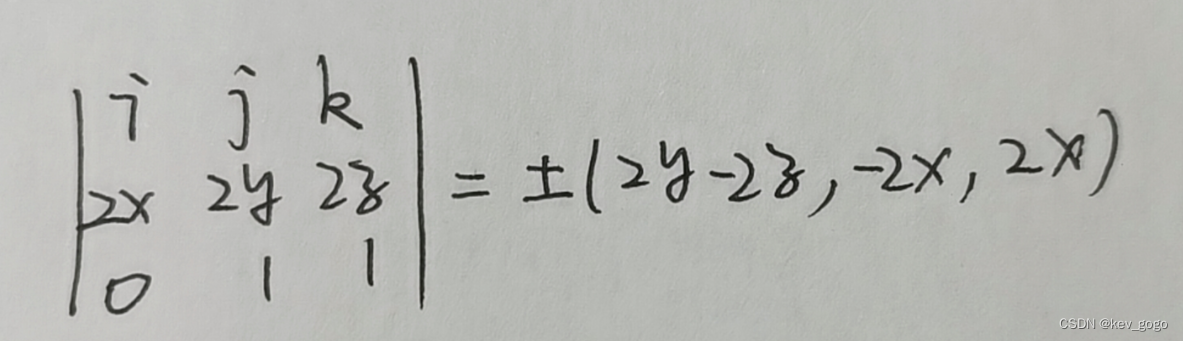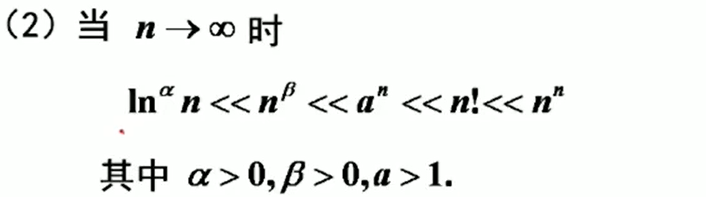华为机试
脑电
ZJSON2ABAPTYPE
存储型XSS
Tableau 技巧
flink 最后一个窗口
网站安全防护
csrf
go
CAPL
cisp题库
storageEvent
TestStand
ldarg
天线
一维高斯函数
薪资
教学研究
宠物猫店管理系统
map
高数
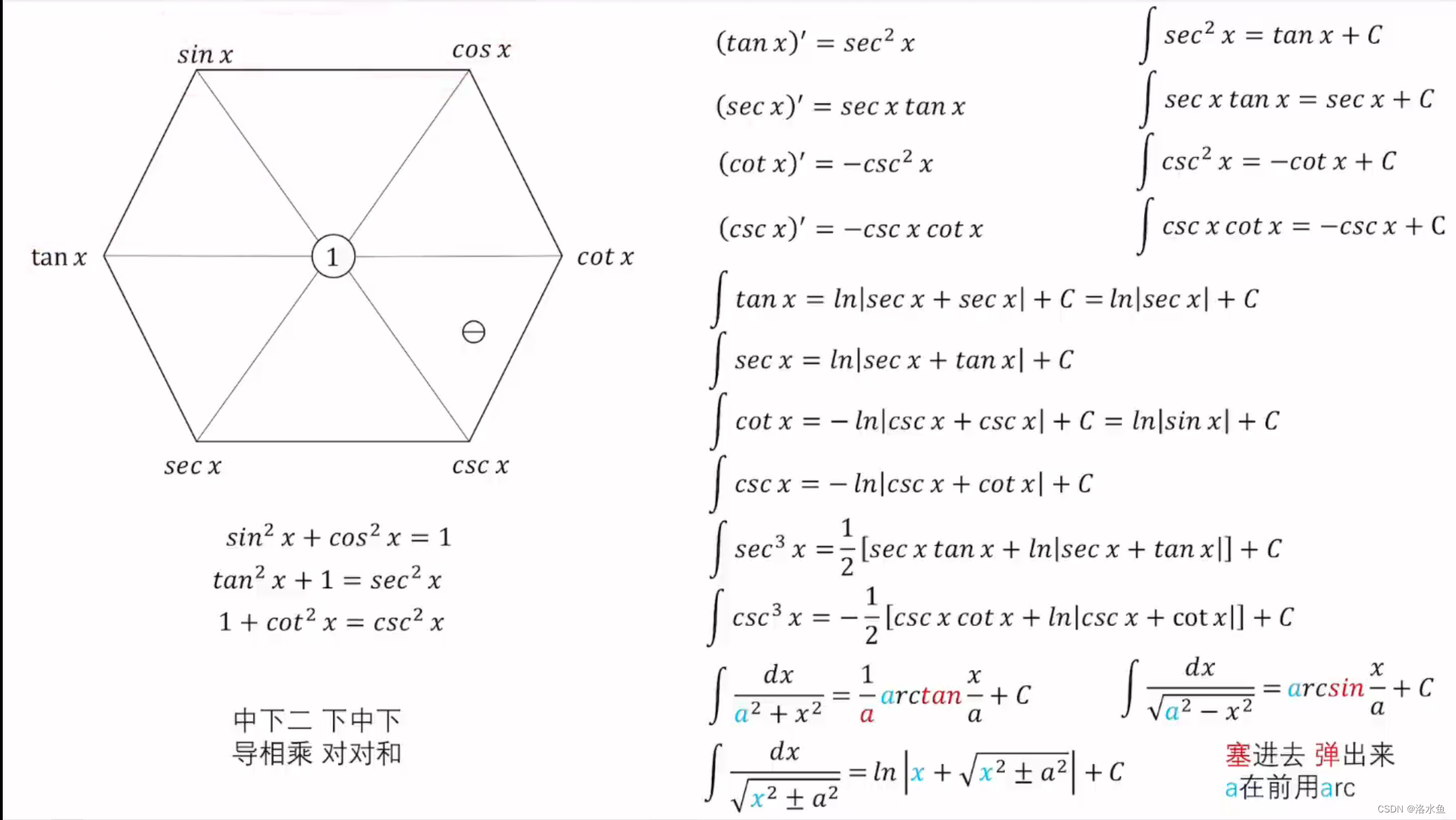
2024/4/11 14:25:52【AI】数学基础——高数(函数微分部分)
参考:https://www.bilibili.com/video/BV1mM411r7ko?p1&vd_source260d5bbbf395fd4a9b3e978c7abde437 唐宇迪:机器学习数学基础 文章目录 1.1 函数1.1.1 函数分类1.1.2 常见函数指/对数函数分段函数原函数&反函数sigmod函数Relu函数(非负函数)复…
可降阶的高阶方程与高阶线性微分方程
目录
可降阶的高阶方程
高阶线性微分方程
齐次方程
非齐次方程 常系数齐次线性微分方程
常系数非齐次线性微分方程 可降阶的高阶方程 我们需要先理解什么是可降解的高阶微分方程。可降解的高阶微分方程是指可以转化为低阶微分方程的方程。 例如,以下是一个二阶…
【专题复习】极值点 拐点 驻点
极值点
基本概念
去心邻域函数值恒大于(小于)该点函数值。
必要条件
当在x0这点取到极值时,且在x0可导,那么导数一定为0。
充分条件
去心左邻域导数值大于(小于)0,去心右邻域导数值小于&a…
专升本高数学习总结——极限
两个重要极限无穷小特点性质等价无穷小替换 两个法则夹逼法则洛必达法则 极限化简的原则左极限与右极限 两个重要极限 无穷小
特点
lima b N (a,b皆为同一趋向下的无穷小) 如果N0,b比a低阶的无穷小,因为b比a大 如果N∞ &…
专升本高数学习总结——函数
本文针对我在学习高数的过程中遇到的个人感觉比较重要的问题所做的总结。 常见初等函数函数特性有界性单调性奇偶性周期性 反函数函数与反函数的关系反函数的求法 三种常用函数的定义域一元二次方程求根方法十字相乘分解求根公式 常见初等函数
幂函数 yx^R R为常数 指数函数…
高数考研 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
函数的四大特性【概念向 + 图片解释】
一、有界性
x在 区间D 上(函数的有界性一定是针对某一区间的),存在
例如,对于函数来说,图像如下所示 当在时,函数有界f(x) < 0.5 x \in (2 , \infty )当时,则函数无界 二、单调性
在定义域…
导数的应用、单调性、极值、最大最小值
函数的单调性 函数的单调性是一个重要的性质,它描述了函数在某个区间上的变化趋势。如果函数在某个区间上单调递增,那么在这个区间上,随着自变量的增大,函数值也会增大;反之,如果函数在某个区间上单调递减&…
【高等数学】微分中值定理
文章目录 1、极值2、费马引理3、罗尔定理4、拉格朗日中值定理4.1用拉格朗日定理证明基本结论 5、柯西中值定理6、微分中值定理的意义7、三大中值定理的意义 1、极值
若 ∃ δ > 0 ∃δ>0 ∃δ>0,使得 ∀ x ∈ U ( x 0 , δ ) ∀x\in U(x_0,δ) ∀x∈U(x0…
【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 1. 对弧长的曲线积分(第一类曲线积分)
文章目录 引言一、曲线积分1.1 对弧长的曲线积分(第一类曲线积分)1. 问题产生 —— 曲线段的质量2. 对弧长曲线积分的定义3. 对弧长的曲线积分的基本性质4. 对弧长的曲线积分的计算方法 写在最后 引言
终于,这应该是高数的最后一个模块了&am…
第一章:极限与连续(常见题型及技巧总结)
文章目录前言一:定义类,主要是极限的定义,记住一个模板就行二:遇带平方或带根号的和差考虑平方差,遇e的一些次方考虑提出来三:两个重要极限的使用四:常见的无穷小五:间断点六&#x…
第八章——向量代数与空间解析几何
目录
一、运算公式
二、平面的法线向量 注:加粗体为向量
一、运算公式
1.若a//b,那么aλb 若a⊥b,那么a*b0
2.若A(x1,y1,z1),B(x2,y2,z2) 中点坐标:AB中点M(x1x2/2,y1y2/2,z1z2/2) 两点间的距离和模的计算&#x…
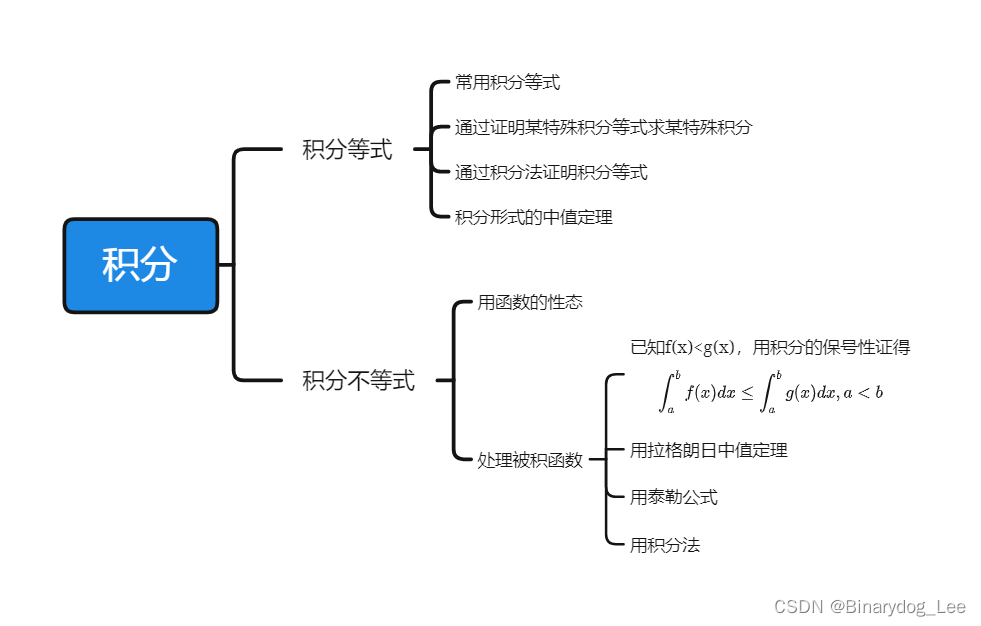
积分等式与积分不等式
参考资料:
B站 - 考研数学-积分不等式(所有方法全归纳)张宇基础和强化及习题册 积分等式
中值定理夹逼准则积分法 在这个专题中,有如下经验:
遇到 f ( x ) f(x) f(x)连续,应当想到变限积分 ∫ a x f ( t…
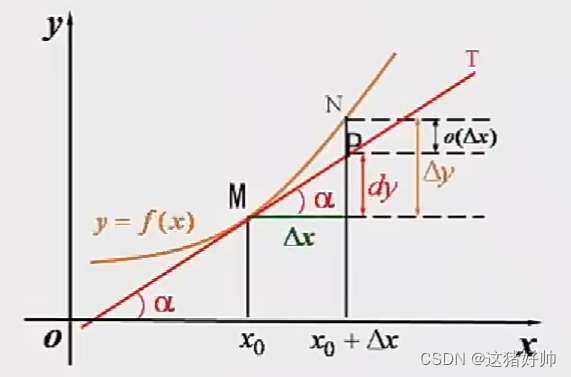
【高等数学】导数与微分
文章目录 1、导数的概念1.1、引例1.1.1、变速直线运动瞬时速度1.1.2、曲线的切线 1.2、导数的定义1.3、证明常用导数1.4、导数的几何意义1.5、可导与连续的关系 2、函数的求导法则2.1、函数的和、差、积、商的求导法则2.2、反函数的求导法则2.3、复合函数的求导法则2.4、基本初…
1.3 向量的数量积与向量积(不做要求)
第三节 向量的数量积与向量积(向量积考纲不作要求)
数量积的概念及运算
定义: 给定两个向量 α , β , \alpha,\beta, α,β,它们的数量积为: α . β ∣ α ∣ ∣ β ∣ cos φ \alpha …
25高数考研张宇 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
【考研数学】数学一“背诵”手册(一)| 高数部分(2)
文章目录 引言一、高数级数空间解析几何球坐标变换公式零碎公式 写在最后 引言
高数一篇文章还是写不太下,再分一些到这里来吧 一、高数
级数
阿贝尔定理:若级数 ∑ a n x n \sum a_nx^n ∑anxn 当 x x 0 xx_0 xx0 时收敛,则适合不…
【问题思考总结】第一型曲线积分和第二型曲线积分的区别与联系【从几何知识的角度思考】
此处为曲面积分------>第一型曲面积分的第二型曲面积分的区别与联系【从几何知识的角度思考】
问题
在做题的时候,我发现,关于这方面的知识有很多很多,但是每道题的解法不尽相似,也没有什么具体的体系,尤其是在结…
第一章 函数 极限 连续(未完更新中)
了解
一、函数的性质 理解
一、函数
1、函数概念 ⚠️定义域和对应规则是同一函数的判断
2、复合函数 简单的说就是内层函数的值域与外层函数的定义域有交集
3、反函数 3.1、yx^3为反函数,yx^2不是
3.2、单调函数是反函数的充分非必要条件(单调函数…
高等数学(三) 极限
极限的概念:
数列的极限 ε和N的作用: ε的作用是为了刻画xn和a的接近程度 N是为了刻画n–>∞大的过程
几何意义: |xn-a|<ε a-ε < xn <aε 数列{Xn}的极限与前有限项无关 函数的极限
自变量趋于无穷大时的函数的极限
lim(x->∞) f(x) A ∀ε > 0, ∃…
【考研数学】数学“背诵”手册 | 需要记忆且容易遗忘的知识点
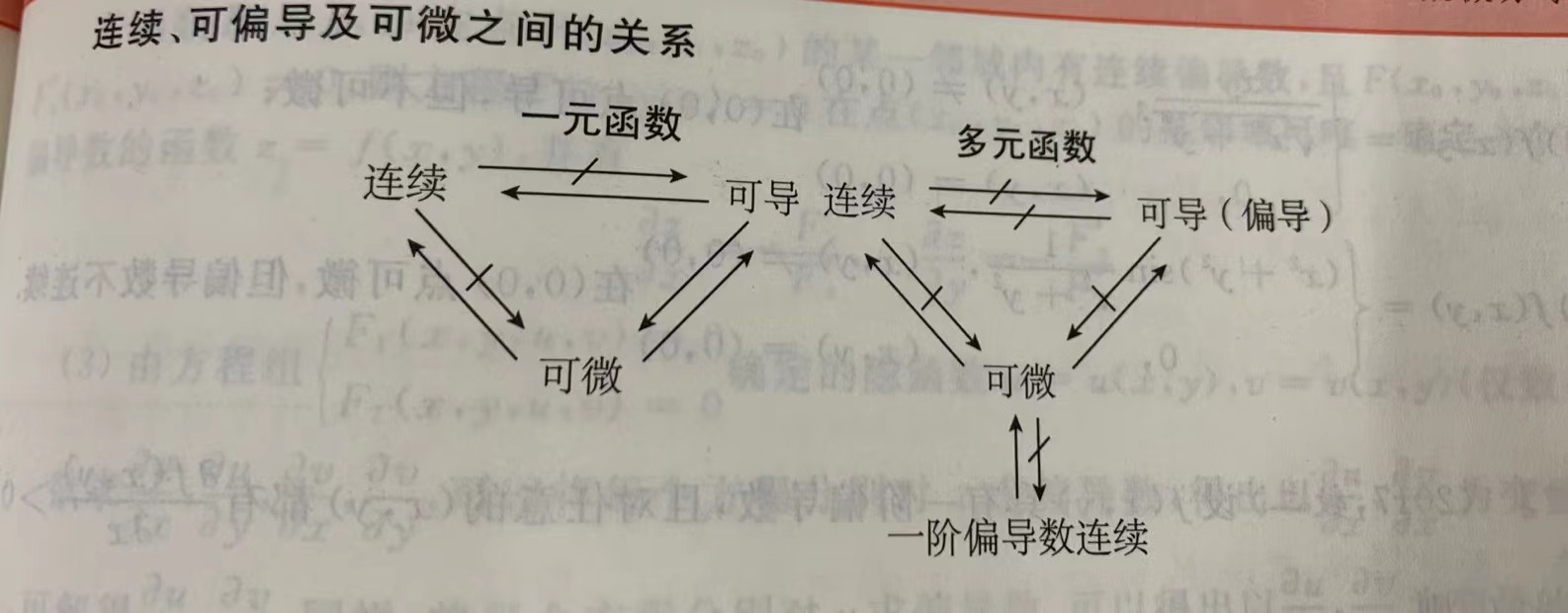
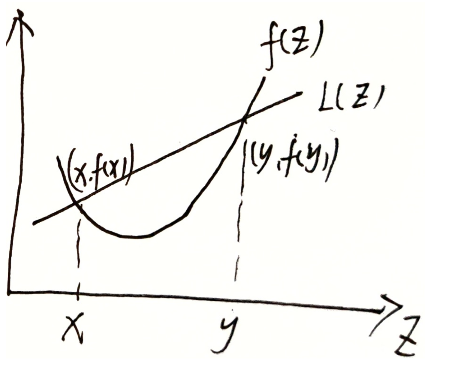
文章目录 引言一、高数常见泰勒展开 n n n 阶导数公式多元微分函数连续、可微、连续可偏导之间的关系多元函数极值无条件极值条件极值 三角函数的积分性质华里士公式( “点火”公式 )特殊性质 原函数与被积函数的奇偶性结论球坐标变换公式 二、写在最后 …
学习高等数学需要的初等数学知识
文章目录 名词解释常用希腊字符读音幂、根式和对数常用的三角函数值三角函数变换一元二次方程求解充分条件和必要条件切线方程、斜率和法线隐函数极坐标排列组合 名词解释
教材中存在着许多熟悉且陌生的词汇,作者在此进行了整理:
概念:概念…
【AI】数学基础——高数(积分部分)
高数(函数&微分部分) 文章目录 1.4 微积分1.4.1 基本思想1.4.2 定积分定义定义计算定积分定积分性质定理N-L公式泰勒公式麦克劳林公式 1.5 求极值1.5.1 无条件极值1.5.2 条件极值1.5.3 多条件极值1.5.4 凹函数与凸函数 1.4 微积分 用于求解速度、面积…